Teori lempeng
Dalam mekanika kontinum , teori lempeng adalah deskripsi matematis dari mekanisme pelat datar yang mengacu pada teori balok . Pelat didefinisikan sebagai pesawat elemen struktur dengan ketebalan kecil dibandingkan dengan dimensi planar. [1] Ketebalan khas terhadap lebar struktur pelat kurang dari 0,1. Sebuah teori pelat mengambil keuntungan dari perbedaan ini dalam skala panjang untuk mengurangi tiga-dimensi penuh mekanika padat masalah untuk masalah dua dimensi. Tujuan dari teori lempeng adalah untuk menghitung deformasi dan tekanan dalam piring dikenai beban.
Dari berbagai teori piring yang telah dikembangkan sejak akhir abad ke-19, dua diterima secara luas dan digunakan dalam rekayasa. Ini adalah- the Kirchhoff - Cinta teori lempeng (plate teori klasik)
- The Mindlin - Reissner teori lempeng (orde pertama teori pelat geser
Teori Kirchhoff-Cinta untuk pelat tipis
The Kirchhoff - Cinta teori merupakan perpanjangan dari Euler-Bernoulli teori balok untuk pelat tipis. Teori ini dikembangkan pada tahun 1888 oleh Cinta [2] menggunakan asumsi yang diusulkan oleh Kirchhoff. Hal ini diasumsikan bahwa pesawat tengah permukaan dapat digunakan untuk mewakili pelat tiga dimensi dalam bentuk dua dimensi.
Asumsi kinematik berikut yang dibuat dalam teori ini: [3] - garis lurus normal ke pertengahan permukaan tetap lurus setelah deformasi
- garis lurus normal ke pertengahan permukaan tetap normal sampai pertengahan-permukaan setelah deformasi
- ketebalan plat tidak berubah selama deformasi
Bidang perpindahan
inat pada pertengahan permukaan pelat pelat badan kaku,
Jika adalah koordinat untuk arah ketebalan,
adalah koordinat untuk arah ketebalan, 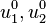 adalah perpindahan dalam bidang pertengahan permukaan, dan
adalah perpindahan dalam bidang pertengahan permukaan, dan  adalah perpindahan dari pertengahan permukaan di
adalah perpindahan dari pertengahan permukaan di  arah.
arah. 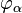 adalah sudut rotasi yang normal sampai pertengahan-permukaan, maka dalam teori Kirchhoff-Love
adalah sudut rotasi yang normal sampai pertengahan-permukaan, maka dalam teori Kirchhoff-Love 
Hubungan regangan-perpindahan
Untuk situasi di mana strain di piring yang sangat kecil dan rotasi normals pertengahan permukaan kurang dari 10 dengan strain-perpindahan hubungan yang
dengan strain-perpindahan hubungan yang
Jika rotasi normals ke pertengahan permukaan berada dalam kisaran 10 15
15  , Hubungan regangan-perpindahan dapat didekati dengan menggunakan von Karman strain. Kemudian asumsi kinematik teori Kirchhoff-Love mengarah pada hubungan regangan-perpindahan berikut
, Hubungan regangan-perpindahan dapat didekati dengan menggunakan von Karman strain. Kemudian asumsi kinematik teori Kirchhoff-Love mengarah pada hubungan regangan-perpindahan berikut
Persamaan Equilibrium
Persamaan kesetimbangan untuk piring dapat diturunkan dari prinsip kerja virtual . Untuk situasi di mana strain dan rotasi piring kecil, persamaan kesetimbangan untuk plat dibongkar diberikan oleh
 . Kuantitas
. Kuantitas  adalah tekanan.
adalah tekanan.
Jika piring dimuat oleh beban didistribusikan eksternal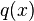 itu normal untuk pertengahan-permukaan dan diarahkan positif
itu normal untuk pertengahan-permukaan dan diarahkan positif  arah, prinsip kerja virtual kemudian mengarah ke persamaan kesetimbangan
arah, prinsip kerja virtual kemudian mengarah ke persamaan kesetimbangan
Kondisi batas
Kondisi batas yang diperlukan untuk memecahkan persamaan kesetimbangan teori plat dapat diperoleh dari istilah batas dalam prinsip kerja virtual.
Untuk strain kecil dan rotasi kecil, kondisi batas yang
 adalah gaya geser yang efektif.
adalah gaya geser yang efektif.
Hubungan tegangan-regangan
Hubungan tegangan-regangan untuk piring Kirchhoff linear elastis yang diberikan oleh
 dan
dan  tidak muncul dalam persamaan kesetimbangan secara implisit diasumsikan
bahwa jumlah ini tidak memiliki efek pada keseimbangan momentum dan
diabaikan.
tidak muncul dalam persamaan kesetimbangan secara implisit diasumsikan
bahwa jumlah ini tidak memiliki efek pada keseimbangan momentum dan
diabaikan.
Hal ini lebih nyaman untuk bekerja dengan stres dan momen hasil yang masuk persamaan kesetimbangan. Hal ini juga terkait dengan pemindahan oleh
Piring Kirchhoff isotropik dan homogen
Artikel utama: Kirchhoff-Love teori pelatUntuk pelat isotropik dan homogen, hubungan tegangan-regangan adalah
Lentur murni
Pemindahan dan
dan 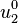 adalah nol bawah lentur murni kondisi. Untuk isotropik, homogen pelat bawah murni lentur persamaan yang mengatur adalah
adalah nol bawah lentur murni kondisi. Untuk isotropik, homogen pelat bawah murni lentur persamaan yang mengatur adalah
Pembebanan transversal
Untuk piring melintang dimuat tanpa deformasi aksial, persamaan yang mengatur memiliki bentuk
 , Persamaan yang mengatur adalah
, Persamaan yang mengatur adalah
Piring Kirchhoff orthotropic dan homogen
Untuk orthotropic plate
Pembebanan transversal
Persamaan yang mengatur piring Kirchhoff orthotropic dimuat melintang oleh beban didistribusikan per satuan luas adalah
per satuan luas adalah
Dinamika tipis pelat Kirchhoff
Artikel utama: Kirchhoff-Love teori pelatTeori dinamis pelat menentukan propagasi gelombang di piring, dan studi gelombang berdiri dan mode getaran.
Persamaan Pemerintahan
Persamaan yang mengatur untuk dinamika piring Kirchhoff-Love adalah
 ,
,
Pelat isotropik
Persamaan yang mengatur menyederhanakan cukup untuk isotropik dan homogen piring yang di-pesawat deformasi dapat diabaikan dan memiliki bentuk adalah kekakuan lentur dari piring. Untuk piring seragam ketebalan
adalah kekakuan lentur dari piring. Untuk piring seragam ketebalan  ,
, Teori Mindlin-Reissner untuk pelat tebal
Artikel utama: Mindlin-Reissner teori pelat
- Catatan: Einstein penjumlahan konvensi penjumlahan pada indeks berulang digunakan di bawah ini.
 dan
dan  menunjuk sudut yang pertengahan permukaan membuat dengan
menunjuk sudut yang pertengahan permukaan membuat dengan  axis kemudian
axis kemudian Hubungan regangan-perpindahan
Tergantung pada jumlah rotasi normals pelat dua pendekatan yang berbeda untuk strain dapat diturunkan dari asumsi dasar kinematik.Untuk strain kecil dan rotasi kecil hubungan regangan-perpindahan untuk pelat Mindlin-Reissner adalah
 ) Diterapkan sehingga jumlah yang benar energi internal yang diprediksi oleh teori. Kemudian
) Diterapkan sehingga jumlah yang benar energi internal yang diprediksi oleh teori. Kemudian Persamaan Equilibrium
Persamaan kesetimbangan memiliki bentuk yang sedikit berbeda tergantung pada jumlah lentur diharapkan piring. Untuk situasi di mana strain dan rotasi piring adalah smallthe persamaan kesetimbangan untuk piring Mindlin-Reissner adalahKondisi batas
Kondisi batas ditunjukkan oleh ketentuan batas dalam prinsip kerja virtual.Jika satu-satunya kekuatan eksternal adalah gaya vertikal pada permukaan atas piring, kondisi batas yang
Hubungan konstitutif
Hubungan tegangan-regangan untuk elastis piring Mindlin-Reissner linear yang diberikan oleh tidak muncul dalam persamaan kesetimbangan secara implisit diasumsikan
bahwa itu tidak memiliki efek pada keseimbangan momentum dan diabaikan. Asumsi ini juga disebut asumsi plane stress. Sisanya hubungan tegangan-regangan untuk bahan orthotropic , dalam bentuk matriks, dapat ditulis sebagai
tidak muncul dalam persamaan kesetimbangan secara implisit diasumsikan
bahwa itu tidak memiliki efek pada keseimbangan momentum dan diabaikan. Asumsi ini juga disebut asumsi plane stress. Sisanya hubungan tegangan-regangan untuk bahan orthotropic , dalam bentuk matriks, dapat ditulis sebagai Isotropik dan homogen piring Mindlin-Reissner
Artikel utama: Mindlin-Reissner teori pelat
Untuk seragam tebal, homogen, isotropik dan pelat, hubungan tegangan-regangan pada bidang piring yang  adalah modulus Young,
adalah modulus Young,  adalah rasio Poisson, dan
adalah rasio Poisson, dan  adalah strain dalam pesawat. Melalui-the-ketebalan tegangan geser dan strain terkait dengan
adalah strain dalam pesawat. Melalui-the-ketebalan tegangan geser dan strain terkait dengan  adalah modulus geser .
adalah modulus geser . Hubungan konstitutif
Hubungan antara resultan tegangan dan perpindahan umum untuk pelat Mindlin-Reissner isotropik adalah: , Kekakuan lentur memiliki bentuk
, Kekakuan lentur memiliki bentuk Persamaan Pemerintahan
Jika kita mengabaikan ekstensi di-pesawat piring, persamaan yang mengatur adalah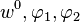 , Tiga persamaan yang mengatur adalah
, Tiga persamaan yang mengatur adalah Teori Reissner-Stein untuk isotropik pelat kantilever
Secara umum, solusi yang tepat untuk plat kantilever menggunakan teori plat cukup terlibat dan solusi yang tepat beberapa dapat ditemukan dalam literatur. Reissner dan Stein [5] memberikan teori disederhanakan untuk pelat kantilever yang merupakan perbaikan atas teori-teori yang lebih tua seperti Saint-Venant teori lempeng.The Reissner-Stein teori mengasumsikan bidang perpindahan melintang dalam bentuk
 , Karena balok dijepit, kondisi batas yang
, Karena balok dijepit, kondisi batas yang  adalah
adalah [ acara ] Penurunan Reissner-Stein persamaan plat kantilever
Referensi
- Timoshenko, S. dan Woinowsky-Krieger, S. "Teori piring dan kerang". McGraw-Hill New York, 1959.
- AEH Love, On getaran bebas kecil dan deformasi kerang elastis, Philosophical trans. dari Royal Society (London), 1888, Vol. série A, N ° 17 p. 491-549.
- Reddy, JN, 2007, Teori dan analisis pelat elastis dan kerang, CRC Press, Taylor dan Francis.
- RD Mindlin, Pengaruh inersia berputar dan geser pada gerakan lentur isotropik, pelat elastis, Journal of Applied Mechanics, 1951, Vol. 18 p. 31-38.
- E. Reissner dan M. Stein. Torsi dan lentur melintang dari pelat kantilever. Catatan Teknis 2369, Komite Penasihat Nasional untuk Aeronautics, Washington, 1951.




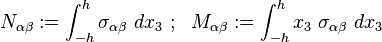

![\ Begin {} menyelaraskan n_ {\ alpha \ beta, \ alpha} & = 0 \ \ M_ {\ alpha \ beta, \ alpha \ beta} + [n_ {\ alpha \ beta} ~ ^ w 0_ {, \ beta} ] _ {\ alpha} - q & = 0 \ end {} menyelaraskan](http://upload.wikimedia.org/math/b/0/5/b0540d0fff760e65355373cbb0cf25f8.png)

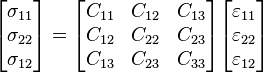



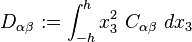
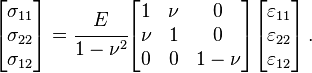


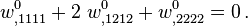



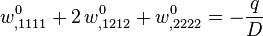

![\ Frac {1} {r} \ cfrac {d} {dr} \ left [r \ cfrac {d} {dr} \ left \ {\ frac {1} {r} \ cfrac {d} {dr} \ left (r \ cfrac {} {} dw dr \ right) \ right \} \ right] = - \ frac {q} {D} \,.](http://upload.wikimedia.org/math/0/6/f/06fb2af0b5690fed73d532b7e5d10e27.png)










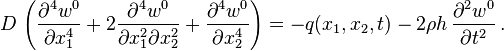














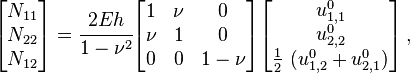


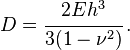







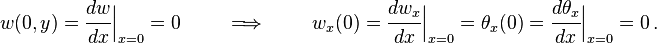
![\ Begin {} menyelaraskan & bD \ cfrac {d ^ 3 w_x} {dx ^ 3} + n_1 (x) \ cfrac {d} {dx} + w_x n_2 (x) \ cfrac {d \ theta_x} {dx} + Q_ {x1} = 0 \ \ & \ frac {b ^ 3D} {12} \ cfrac {d ^ 3 \ theta_x} {dx ^ 3} + \ left [n_3 (x)-2BD (1 - \ nu) \ kanari] \ cfrac {d \ theta_x} {dx} + n_2 (x) \ cfrac {d} {dx} + w_x t = 0 \ \ & bD \ cfrac {d ^ 2} {dx w_x ^ 2} + m_1 = 0 \ quad, \ quad \ frac {b ^ 3D} {12} \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} + m_2 = 0 \ end {} menyelaraskan](http://upload.wikimedia.org/math/1/9/b/19bf7f6399a56fd48e62e871c4957a49.png)

Tidak ada komentar:
Posting Komentar