welcome to the my blog

matursuwun sing katah

Kamis, 02 Oktober 2014

Fungsi dan cara kerja rem cakram (req septian )

Kaliper rem merupakan bagian sistem rem yang tugasnya mencengkram disc motor adatu piringan cakram yang menyatu roda sehingga putaran roda bisa berhenti. Sistem kerjanya tergantung dari tekanan hidrolik master cakram. Tekanan hidrolik ini akan menekan piston dan kampas rem sehingga akan menjepit cakram. Kaliper rem terdiri dari komponen chasing, piston, serta bantalan rem/kampas rem. Piston biasanya dibuat dari alumunium atau besi berlapis hard chrome. Ada dua tipe kaliper, terapung atau tetap. Kaliper tetap tidak bergerak relatif terhadap cakram. Tipe ini menggunakan satu atau banyak piston untuk menekan masing-masing sisi piringan cakram. Kaliper terapung (atau disebut kaliper sliding) bergerak searah dengan cakram. Sebuah piston pada satu sisi cakram mendorong kampas rem dalam hingga membuat sentuhan dengan permukaan piringan cakram. Kemudian mendorong bodi kaliper dengan bantalan rem luar sehingga tekanan terjadi pada kedua sisi piringan cakram.
Kelebihan aplikasi kaliper cakram
Kelebihan aplikasi kaliper cakram dapat bekerja di berbagai suhu, sehingga hampir semua kendaraan menerapkan sistem rem cakram sebagai andalannya. Selain itu kaliper cakram tahan terhadap genangan air sehingga pada kendaraan yang telah menggunakan rem cakram dapat menerjang banjir dengan aman. Memiliki sistem pendingin luar (terbuka) sehingga pendinginan terbilang lebih efektif.
Kekurangan aplikasi kaliper cakram
Kekurangan aplikasi kaliper cakram Sifatnya yang terbuka memudahkan debu dan lumpur menempel, lama kelamaan lumpu/ kotoran tersebut dapat menghambat kinerja pengereman sampai merusak pada bagian komponen pada bagian kaliper seperti piston bila dibiarkan lama. Oleh sebab itu perlu dilakukan pembersihan sesering mungkin
@patan
Diposting oleh di Tidak ada komentar:

PERJALANAN TEKNOLOGI REM MOTOR


Rem berfungsi untuk mengurangi kecepatan dan menghentikan laju motor. Bahkan beberapa motor rakitan sekarang ada yang memanfaatkannya untuk parkir di tempat agak menurun, seperti di Honda BeAT.
Rem sendiri bekerja atas dasar pemanfaatan gaya gesek. Maksudnya putaran roda dijepit kampas. Tentunya yang dijepit teromol atau cakramnya. Makanya roda bisa berhenti.
Pada rem discs (disc brake) yang dijepit kampas yaitu cakramnya. Sedangkan di rem teromol atau drum brake yang dijepit teromolnya. Sehingga terjadi gesekan yang kuat membuat roda berhenti.
Namun seiring perkembangan yang berazas pada efisiensi ruang dan tetap meningkatkan performanya, perangkat ciet terus dibenahi. Motor yang awalnya pakai rem teromol dan beralih ke cakram, kini fiturnya lebih menarik.
Berikut info soal rem dan fitur perkembangannya.
REM CAKRAM (DISC BRAKE) – Lebih pakem dibanding teromol.
Berbeda dengan rem teromol, untuk mengoperasikan rem cakram perlu beberapa komponen yang model dan bentuknya berbeda dengan rem teromol. Setidaknya ada lima komponen penting, diantaranya master rem, slang, kaliper, kampas, piringan dan minyak rem.
Mulai dari paling atas master rem berfungsi sebagai penekan minyak rem. Karena sistem kerja dari rem cakram menekankan minyak rem terhadap kaliper rem. Sedangkan di dalam master terdapat beberapa komponen seperti bak kecil penampung minyak rem, handel penekan piston dan pegas pembalik handel.
Wadah master rem befungsi sebagai pembuka dan penutup lubang aliran minyak rem. Itu agar piston master rem bisa menekan minyak rem menuju slang ke arah kaliper.
Setelah master rem, di bagian bawah terdapat slang rem berbahan karet khusus yang berfungsi sebagai penghubung aliran minyak rem yang kemudian berlanjut ke kaliper. “Di kaliper punya batang penekan berupa piston. Fungsinya untuk menekan kampas rem agar dapat menjepit cakram atau piringan,” terang Firman Mansur, mekanik bengkel umum Laris Motor di Jl.Raya Kamasan No.241, Banjaran Bandung.
Piston kaliper tidak bersinggungan langsung dengan cakram, tapi daya dorong piston ke kampas berbentuk kotak itu yang akan menekan dan bergesekan dengan cakram.
Biar pakem, kampas rem model cakram biasanya terbuat dari campuran asbes dan material khusus lain yang dibentuk sedemikian rupa agar bisa menekan atau menjepit cakram.
Tekanan piston ke kampas rem dan berakhir di piringan jelas bukan hanya satu bagian. Agar kerjanya sempurna dan kuat menjepit piringan, salah satu bagian kampas juga ditempatkan di kaliper yang ada di antara piringan. Komponen penting lain adalah minyak rem.
REM TEROMOL (DRUM BRAKE) – CARA KERJA REM TEROMOL
Pada drum brake, kekuatan tenaga pengereman diperlukan dari dua sepatu kampas yang bentuk setengah lingkaran. Kedua kampas yang terpasang di panel rem teromol secara terpisah sehingga membentuk seperti lingkaran. Lalu masing-masing bagian ujung kedua kampas terikat dengan pegas pembalik.
Cara kerja rem ini, dimulai dari tuas rem di setang ditarik. Kabel menarik as pengungkit di panel rem. “Maka kedua ujung kampas yang permukaannya rata dan awalnya diam, lalu menekan pada permukaan teromol bagian dalam yang berputar bersama roda. Saat itulah proses pengereman sedang berlangsung,” ujar Yunarto dari dealer Honda AHASS 07592 Bintang Motor.
Lanjut mekanik di Jl.Limo Cinere, Depok itu, teromol rem yang berputar bersama roda letaknya sangat dekat dengan kampas rem. Makanya saat tuas rem tidak ditarik, kedua kampas tidak saling bersentuhan. Sebab di kedua kampas yang menapak di as diam dan berputar terdapat pegas pembalik.
Oh iya, kekuatan pengereman pada rem tipe teromol bukan hanya tergantung pada kampas rem yang baik, tapi juga dari kekuatan jari tangan menarik tuas rem dan kekakuan kabel rem. Kalau tarikannya lemas, kemampuan rem pun menyesuaikan.
Kelemahan rem teromol tidak sekuat rem cakram. Makanya sekarang hanya digunakan pada rem belakang. Supaya roda belakang tidak mengunci cukup pakai rem teromol ini.
ABS (ANTI-LOCK BRAKING SYSTEM)
Rem yang ada sekarang tidak sebatas hanya menghentikan laju motor, tapi juga dirancang mendukung keselamatan pengendara. Salah satunya teknologi rem ABS (Anti-Lock Braking System). Lebih dulu digunakan perusahaan mobil merek BMW. Dan seiring perkembangannya, perangkat ini pun digunakan pada kendaraan roda dua.
Di Indonesia, saat ini motor yang sudah menggunakan rem ABS diantaranya Honda CBR 250R dan Kawasaki Ninja 250. Meski secara teknis kerjanya sama, tapi dua pabrikan itu memberikan nama dan fitur berbeda.
Nah, buat panduan coba dibahas rem ABS yang digunakan di Ninja 250. Teknologinya penyesuaian dari yang dianut motor pendahulunya, yaitu Kawasaki ZX 1400F.
“Tapi karena sasis dan tempat modulatornya tidak terlalu besar, makanya bentuknya dibikin lebih kecil. Ditempatkan di bawah tangki,” kata Freddyanto Basuki, Manajer Marketing dan Promosi PT Kawasaki Motor Indonesia (KMI). Modulator yang dimaksud alat pengukur tekanan cairan di dalam kaliper, agar tekanan piston ke cakram roda depan tidak mengunci ketika mengerem mendadak.
Namun ABS yang diterapkan di New Ninja tidak hanya di cakram depan saja, melainkan juga di belakang. Seperti semua tahu, pengendara motor akan lebih banyak menggunakan rem depan dibanding belakang. Sehingga ABS memiliki prosentase 40% di belakang.
Cara kerja modulator ABS New Ninja 250 berpatokan pada sensor yang ada di dekat kaliper rem. Tugas sensor membaca percepatan ring ABS, untuk dilaporkan ke ECU (Elektronic Control Unit) pengontrol ABS yang dibuat terpisah dari ECU central. Tapi, semuanya berhubungan dan tetap dikontrol oleh ECU central.
Jadi, simplenya sensor ABS akan membaca perputaran ring cakram. Hasil sensor berbentuk data akan diteruskan ke ECU ABS, lanjut ke ECU central, dan akan mengomandoi modulator melakukan pengereman sebanyak 60% dan 40% tadi. Sistem modulator ini berupa katup yang membuka dan menutup.
“Hasilnya bila pengereman secara mendadak, roda tidak akan ngelock atau mengunci, karena semua sudah diprogram dan diatur oleh ECU. Kinerja ABS ini juga bisa di programable agar kinerjanya bisa dikondisikan sesuai kebutuhan,” kata Fredy sapaan akrabnya.
REM CBS (COMBI BRAKE SYSTEM)
Kalau tahu cara kerja rem Combi Brake System (CBS), mungkin maknanya hampir sama dengan pepatah “Sambil menyelam minum air”. Maksudnya, sistem kerja rem yang pakai satu tuas tapi bisa melakukan dua fungsi pengereman secara bersamaan.
“Jelas ketika tuas rem belakang ditekan, secara otomatis rem depan pun akan melakukan pengereman,” buka Sukarman, kepala mekanik bengkel resmi Honda Setia Utama Motor.
Walaupun kedua rem dapat bekerja secara bersamaan, namun brother tidak perlu khawatir kedua rem bakal ngerem sama kuatnya. Karena porsi antara rem depan dan belakang dikomposisikan berbeda. “Perbandingannya sekitar 30% rem depan dan 70% rem belakang,” bilang pria yang bengkelnya berada di Jl.HOS Cokroaminoto No.5, Ciledug, Tangerang.
Agar fungsi seperti itu, teknologi yang hanya ada di Honda Vario Techno, Honda Vario 125 PGM-FI dan Honda All New BeAT FI didukung perangkat bernama Equalizer. Jelasnya, ketika tuas rem belakang ditekan, salah satu cabang kabel dari tuas rem belakang akan menarik equalizer yang juga bercabang ke master rem depan.
Jadi ketika tuas rem belakang ditekan, equalizer itu dapat menarik satu kabel langsung ke rem belakang dan satu kabel lagi ke kabel konektor rem depan. “Nah, kabel konektor ini akan menarik knocker untuk mendorong piston hidrolik di master rem depan,” tambah Sukarman.
source: motor plus

Diposting oleh di Tidak ada komentar:

Sistem Dan penjelasan pengereman sepeda motor BAG 1.


Kita sudah tahu bahwa sistem pengereman pada sepeda motor adalah hal yang sangat penting untuk kita ketahui tapi banyak dari kita kita termasuk saya yng belum paham akan sistem mekanisme pengereman ,di sini kita akan belajar mengenai jenis dan penjelasannya dari pengereman sepeda motor


1. Drum brake ( Rem tromol )
Rem tromol merupakan sistem rem yang telah menjadi metode pengereman standar yang digunakan sepeda motor kapasitas kecil pada beberapa tahun belakangan ini. Alasannya adalah karena rem tromol sederhana dan murah. Konstruksi rem tromol umumnya terdiri dari komponen-komponen seperti: sepatu rem (brake shoe), tromol (drum), pegas pengembali (return springs), tuas penggerak (lever), dudukan rem tromol (backplate), dan cam/nok penggerak. Cara pengoperasian rem tromol pada umumnya secara mekanik yang terdiri dari; pedal rem (brake pedal) dan batang (rod) penggerak.
Pada saat kabel atau batang penghubung (tidak ditarik), sepatu rem dan tromol tidak saling kontak. Tromol rem berputar bebas mengikuti putaran roda.Tetapi saat kabel rem atau batang penghubung ditarik, lengan rem atau tuas rem memutar cam/nok pada sepatu rem sehingga sepatu rem menjadi mengembang dan kanvas rem (pirodo)nya bergesekan dengan tromol. Akibatnya putaran tromol dapat ditahan atau dihentikan, dan ini juga berarti menahan atau menghentikan putaran roda.
Rem tromol terbuat dari besi tuang dan digabung dengan hub saat rem digunakan sehingga panas gesekan akan timbul dan gaya gesek dari brake lining dikurangi. Drum brake mempunyai sepatu rem (dengan lining) yang berputar berlawanan dengan putaran drum (wheel hub) untuk mengerem roda dengan gesekan. Pada sistem ini terjadi gesekangesekan sepatu rem dengan tromol yang akan memberikan hasil energi panas sehingga bisa menghentikan putaran tromol tersebut. Rem tromol disebut “internal expansion lining brake”
Kelebihan rem tromol
  • Murah ongkos produksi
  • Cocok untuk motor ber CC kecil
  • Parts nya mudah di temukan
  • Kinerja rem tromol lebih lembut
Kekurangan rem tromol
  • Daya pengeremannya tidak mencapai 70%
  • kotoran yang masuk akan sulit keluar dan akan menyebabkan bunyi yang tidak nyaman

2. Disk brake (rem cakram)
Penjelasan : Rem cakram adalah perangkat pengereman yang digunakan pada kendaraan modern. Rem ini bekerja dengan menjepit cakram yang biasanya dipasangkan pada roda kendaraan, untuk menjepit cakram digunakan caliper yang digerakkan oleh piston untuk mendorong sepatu rem (brake pads) ke cakram. Rem jenis ini juga digunakan pada kereta api,mobil,sepeda
Cara kerja : Kaliper rem merupakan bagian sistem rem yang tugasnya mencengkram disc motor adatu piringan cakram yang menyatu roda sehingga putaran roda bisa berhenti. Sistem kerjanya tergantung dari tekanan hidrolik master cakram. Tekanan hidrolik ini akan menekan piston dan kampas rem sehingga akan menjepit cakram. Kaliper rem terdiri dari komponen chasing, piston, serta bantalan rem/kampas rem. Piston biasanya dibuat dari alumunium atau besi berlapis hard chrome. Ada dua tipe kaliper, terapung atau tetap. Kaliper tetap tidak bergerak relatif terhadap cakram. Tipe ini menggunakan satu atau banyak piston untuk menekan masing-masing sisi piringan cakram. Kaliper terapung (atau disebut kaliper sliding) bergerak searah dengan cakram. Sebuah piston pada satu sisi cakram mendorong kampas rem dalam hingga membuat sentuhan dengan permukaan piringan cakram. Kemudian mendorong bodi kaliper dengan bantalan rem luar sehingga tekanan terjadi pada kedua sisi piringan cakram.
Kelebihan rem cakram
  • rem cakram dapat di gunakan di kawasan dengan suhu rendah hingga tinggi
  • tahan terhadap genangan air
  • gaya pengereman bisa mencapai 100%
Kekurangan rem cakram
  • Debu mudah menempel dan lama-kelamaan akan mengeras,debu yang mengeras dapat mengurangi kinerja rem
Diposting oleh di Tidak ada komentar:

Kamis, 24 April 2014

tentang plat dan shell

Teori lempeng

Dalam mekanika kontinum , teori lempeng adalah deskripsi matematis dari mekanisme pelat datar yang mengacu pada teori balok . Pelat didefinisikan sebagai pesawat elemen struktur dengan ketebalan kecil dibandingkan dengan dimensi planar. [1] Ketebalan khas terhadap lebar struktur pelat kurang dari 0,1. Sebuah teori pelat mengambil keuntungan dari perbedaan ini dalam skala panjang untuk mengurangi tiga-dimensi penuh mekanika padat masalah untuk masalah dua dimensi. Tujuan dari teori lempeng adalah untuk menghitung deformasi dan tekanan dalam piring dikenai beban.

Dari berbagai teori piring yang telah dikembangkan sejak akhir abad ke-19, dua diterima secara luas dan digunakan dalam rekayasa. Ini adalah
  • the Kirchhoff - Cinta teori lempeng (plate teori klasik)
  • The Mindlin - Reissner teori lempeng (orde pertama teori pelat geser

    Teori Kirchhoff-Cinta untuk pelat tipis

    The Kirchhoff - Cinta teori merupakan perpanjangan dari Euler-Bernoulli teori balok untuk pelat tipis. Teori ini dikembangkan pada tahun 1888 oleh Cinta [2] menggunakan asumsi yang diusulkan oleh Kirchhoff. Hal ini diasumsikan bahwa pesawat tengah permukaan dapat digunakan untuk mewakili pelat tiga dimensi dalam bentuk dua dimensi.

    Asumsi kinematik berikut yang dibuat dalam teori ini: [3]
  • garis lurus normal ke pertengahan permukaan tetap lurus setelah deformasi
  • garis lurus normal ke pertengahan permukaan tetap normal sampai pertengahan-permukaan setelah deformasi
  • ketebalan plat tidak berubah selama deformasi

    Bidang perpindahan

    inat pada pertengahan permukaan pelat pelat badan kaku, x_3 adalah koordinat untuk arah ketebalan, u ^ 0_1, u ^ 0_2 adalah perpindahan dalam bidang pertengahan permukaan, dan w ^ 0 adalah perpindahan dari pertengahan permukaan di x_3 arah.

    Jika \ Varphi_ \ alpha adalah sudut rotasi yang normal sampai pertengahan-permukaan, maka dalam teori Kirchhoff-Love \ Varphi_ \ alpha = w ^ 0_ {, \ alpha} \,.
    Perpindahan dari pertengahan permukaan (kiri) dan normal (kanan)

    Hubungan regangan-perpindahan

    Untuk situasi di mana strain di piring yang sangat kecil dan rotasi normals pertengahan permukaan kurang dari 10 ^ \ CIRC dengan strain-perpindahan hubungan yang
    \ Begin {} menyelaraskan \ varepsilon_ {\ alpha \ beta} & = \ tfrac {1} {2} (u ^ 0_ {\ alpha, \ beta} + u ^ 0_ {\ beta, \ alpha}) - x_3 ~ w ^ 0_ {, \ alpha \ beta} \ \ \ varepsilon_ {\ alpha} 3 & = - w ^ 0_ {, \ alpha} + {w ^ 0_, \ alpha} = 0 \ \ \ varepsilon_ {33} & = 0 \ end {} menyelaraskan
    Oleh karena itu satu-satunya strain non-nol berada di arah in-plane.
    Jika rotasi normals ke pertengahan permukaan berada dalam kisaran 10 ~ ^ {\ CIRC} 15 ^ \ CIRC , Hubungan regangan-perpindahan dapat didekati dengan menggunakan von Karman strain. Kemudian asumsi kinematik teori Kirchhoff-Love mengarah pada hubungan regangan-perpindahan berikut
    \ Begin {} menyelaraskan \ varepsilon_ {\ alpha \ beta} & = \ frac {1} {2} (u ^ 0_ {\ alpha, \ beta} + u ^ 0_ {\ beta, \ alpha} + {w ^ 0_ , \ alpha} ~ ^ w 0_ {, \ beta}) - x_3 ~ ^ w 0_ {, \ alpha \ beta} \ \ \ varepsilon_ {\ alpha} 3 & = - w ^ 0_ {, \ alpha} + w ^ 0_ {, \ alpha} = 0 \ \ \ varepsilon_ {33} & = 0 \ end {} menyelaraskan
    Teori ini tidak linier karena istilah kuadrat dalam hubungan regangan-perpindahan.

    Persamaan Equilibrium

    Persamaan kesetimbangan untuk piring dapat diturunkan dari prinsip kerja virtual . Untuk situasi di mana strain dan rotasi piring kecil, persamaan kesetimbangan untuk plat dibongkar diberikan oleh
    \ Begin {} menyelaraskan n_ {\ alpha \ beta, \ alpha} & = 0 \ \ M_ {\ alpha \ beta, \ alpha \ beta} & = 0 \ end {} menyelaraskan
    di mana resultan tegangan dan resultants saat stres didefinisikan sebagai
    N_ {\ alpha \ beta}: = \ int_ {-h} ^ h \ sigma_ {\ alpha \ beta} ~ ~ dx_3; ~ ~ M_ {\ alpha \ beta}: = \ int_ {-h} ^ h x_3 ~ \ sigma_ {\ alpha \ beta} ~ dx_3
    dan ketebalan pelat adalah 2h . Kuantitas \ Sigma_ {\ alpha \ beta} adalah tekanan.
    Jika piring dimuat oleh beban didistribusikan eksternal q (x) itu normal untuk pertengahan-permukaan dan diarahkan positif x_3 arah, prinsip kerja virtual kemudian mengarah ke persamaan kesetimbangan
    \ Begin {} menyelaraskan n_ {\ alpha \ beta, \ alpha} & = 0 \ \ M_ {\ alpha \ beta, \ alpha \ beta} - q & = 0 \ end {} menyelaraskan
    Untuk rotasi moderat, hubungan regangan-perpindahan berbentuk von Karman dan persamaan kesetimbangan dapat dinyatakan sebagai
    \ Begin {} menyelaraskan n_ {\ alpha \ beta, \ alpha} & = 0 \ \ M_ {\ alpha \ beta, \ alpha \ beta} + [n_ {\ alpha \ beta} ~ ^ w 0_ {, \ beta} ] _ {\ alpha} - q & = 0 \ end {} menyelaraskan

    Kondisi batas

    Kondisi batas yang diperlukan untuk memecahkan persamaan kesetimbangan teori plat dapat diperoleh dari istilah batas dalam prinsip kerja virtual.
    Untuk strain kecil dan rotasi kecil, kondisi batas yang
    \ Begin {} menyelaraskan n_ \ alpha ~ n_ {\ alpha \ beta} & \ quad \ mathrm {atau} \ quad u ^ 0_ \ beta \ \ n_ \ alpha ~ M_ {\ alpha \ beta, \ beta} & \ quad \ mathrm {atau} \ quad w ^ 0 \ \ n_ \ beta ~ M_ {\ alpha \ beta} & \ quad \ mathrm {atau} \ quad w ^ 0_ {, \ alpha} \ end {} menyelaraskan
    Perhatikan bahwa kuantitas n_ \ alpha ~ M_ {\ alpha \ beta, \ beta} adalah gaya geser yang efektif.

    Hubungan tegangan-regangan

    Hubungan tegangan-regangan untuk piring Kirchhoff linear elastis yang diberikan oleh
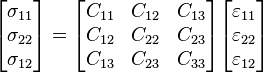
    \ Begin {bmatrix} \ {11} sigma_ \ \ \ sigma_ {22} \ \ \ sigma_ {12} \ end {bmatrix} = \ begin {bmatrix} C_ {11} & C_ {12} & C_ {13} \ \ C_ {12} & C_ {22} & C_ {23} \ \ C_ {13} & C_ {23} & C_ {33} \ end {bmatrix} \ begin {bmatrix} \ {11} varepsilon_ \ \ \ varepsilon_ {22} \ \ \ varepsilon_ {12} \ end {bmatrix}
    Karena \ Sigma_ {\ alpha 3} dan \ Sigma_ {33} tidak muncul dalam persamaan kesetimbangan secara implisit diasumsikan bahwa jumlah ini tidak memiliki efek pada keseimbangan momentum dan diabaikan.
    Hal ini lebih nyaman untuk bekerja dengan stres dan momen hasil yang masuk persamaan kesetimbangan. Hal ini juga terkait dengan pemindahan oleh
    \ Begin {bmatrix} n_ {11} \ \ n_ {22} \ \ n_ {12} \ end {bmatrix} = \ left \ {\ {int_-h} ^ h \ begin {bmatrix} C_ {11} & C_ {12} & C_ {13} \ \ C_ {12} & C_ {22} & C_ {23} \ \ C_ {13} & C_ {23} & C_ {33} \ end {bmatrix} ~ dx_3 \ right \ } \ begin {bmatrix} u ^ 0_ {1,1} \ \ u ^ 0_ {2,2} \ \ \ frac {1} {2} ~ (u ^ 0_ {1,2} + u ^ 0_ {2 , 1}) \ end {bmatrix}
    dan
    \ Begin {bmatrix} M_ {11} \ \ M_ {22} \ \ M_ {12} \ end {bmatrix} = - \ left \ {\ {int_-h} ^ h x_3 ^ 2 ~ \ begin {bmatrix} C_ {11} & C_ {12} & C_ {13} \ \ C_ {12} & C_ {22} & C_ {23} \ \ C_ {13} & C_ {23} & C_ {33} \ end {bmatrix} ~ dx_3 \ right \} \ begin {bmatrix} w ^ 0_ {, 11} \ \ w ^ 0_ {, 22} \ \ w ^ 0_ {, 12} \ end {bmatrix} \,.
    The kekakuan ekstensional adalah jumlah
    A_ {\ alpha \ beta}: = \ int_ {-h} ^ h C_ {\ alpha \ beta} ~ dx_3
    The kekakuan lentur (juga disebut kekakuan lentur) adalah jumlah
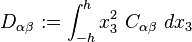
    D_ {\ alpha \ beta}: = \ int_ {-h} ^ h x_3 ^ 2 ~ C_ {\ alpha \ beta} ~ dx_3

    Piring Kirchhoff isotropik dan homogen

    Artikel utama: Kirchhoff-Love teori pelat
    Untuk pelat isotropik dan homogen, hubungan tegangan-regangan adalah
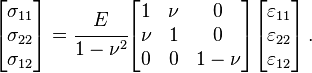
    \ Begin {bmatrix} \ {11} sigma_ \ \ \ sigma_ {22} \ \ \ sigma_ {12} \ end {bmatrix} = \ cfrac {E} {1 - \ nu ^ 2} \ begin {bmatrix} 1 & \ nu & 0 \ \ \ nu & 1 & 0 \ \ 0 & 0 & 1 - \ nu \ end {bmatrix} \ begin {bmatrix} \ {11} varepsilon_ \ \ \ varepsilon_ {22} \ \ \ varepsilon_ {12 } \ end {bmatrix} \,.
    Saat-saat yang sesuai dengan tegangan ini
    \ Begin {bmatrix} M_ {11} \ \ M_ {22} \ \ M_ {12} \ end {bmatrix} = - \ cfrac {2h ^ 3E} {3 (1 - \ nu ^ 2)} ~ \ begin { bmatrix} 1 & \ nu & 0 \ \ \ nu & 1 & 0 \ \ 0 & 0 & 1 - \ nu \ end {bmatrix} \ begin {bmatrix} w ^ 0_ {, 11} \ \ w ^ 0_ {, 22} \ \ w ^ 0_ {, 12} \ end {bmatrix}

    Lentur murni

    Pemindahan u ^ 0_1 dan u ^ 0_2 adalah nol bawah lentur murni kondisi. Untuk isotropik, homogen pelat bawah murni lentur persamaan yang mengatur adalah
    \ Frac {\ partial ^ 4 w} {\ x_1 parsial ^ 4} + 2 \ frac {\ partial ^ 4 w} {\ x_1 parsial ^ 2 \ x_2 parsial ^ 2} + \ frac {\ partial ^ 4 w} { \ x_2 parsial ^ 4} = 0 \ quad \ text {} di mana \ quad w: w = ^ 0 \,.
    Dalam notasi indeks,
    w ^ 0_ {, 1111} + 2 ~ ^ w 0_ {, 1212} + {w ^ 0_, 2222} = 0 \,.
    Dalam notasi tensor langsung, persamaan yang mengatur adalah
    \ Nabla ^ 2 \ nabla ^ 2 w = 0 \,.

    Pembebanan transversal

    Untuk piring melintang dimuat tanpa deformasi aksial, persamaan yang mengatur memiliki bentuk
    \ Frac {\ partial ^ 4 w} {\ x_1 parsial ^ 4} + 2 \ frac {\ partial ^ 4 w} {\ x_1 parsial ^ 2 \ x_2 parsial ^ 2} + \ frac {\ partial ^ 4 w} { \ x_2 parsial ^ 4} = - \ frac {q} {D}
    dimana
    D: = \ cfrac {2h ^ 3E} {3 (1 - \ nu ^ 2)} \,.
    Dalam notasi indeks,
    w ^ 0_ {, 1111} + 2 \, w ^ 0_ {, 1212} + {w ^ 0_, 2222} = - \ frac {q} {D}
    dan dalam notasi langsung
    \ Nabla ^ 2 \ nabla ^ 2 w = - \ frac {q} {D} \,.
    Dalam koordinat silinder (R, \ theta, z) , Persamaan yang mengatur adalah
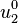
    \ Frac {1} {r} \ cfrac {d} {dr} \ left [r \ cfrac {d} {dr} \ left \ {\ frac {1} {r} \ cfrac {d} {dr} \ left (r \ cfrac {} {} dw dr \ right) \ right \} \ right] = - \ frac {q} {D} \,.

    Piring Kirchhoff orthotropic dan homogen

    Untuk orthotropic plate
    \ Begin {bmatrix} C_ {11} & C_ {12} & C_ {13} \ \ C_ {12} & C_ {22} & C_ {23} \ \ C_ {13} & C_ {23} & C_ {33 } \ end {bmatrix} = \ cfrac {1} {1 - \ nu_ {12} \ nu_ {21}} \ begin {bmatrix} E_1 & \ nu_ {12} E_2 & 0 \ \ \ nu_ {21} E_1 & E_2 & 0 \ \ 0 & 0 & 2G_ {12} (1 - \ nu_ {12} \ {21} nu_) \ end {bmatrix} \,.
    Oleh karena itu,
    \ Begin {bmatrix} A_ {} 11 & A_ {} 12 & A_ {} 13 \ \ A_ {} 21 & A_ {} 22 & A_ {} 23 \ \ A_ {} 31 & A_ {} 32 & A_ {33 } \ end {bmatrix} = \ cfrac {2h} {1 - \ nu_ {12} \ nu_ {21}} \ begin {bmatrix} E_1 & \ nu_ {12} E_2 & 0 \ \ \ nu_ {21} E_1 & E_2 & 0 \ \ 0 & 0 & 2G_ {12} (1 - \ nu_ {12} \ {21} nu_) \ end {bmatrix}
    dan
    \ Begin {bmatrix} D_ {11} & D_ {12} & D_ {13} \ \ D_ {21} & D_ {22} & D_ {23} \ \ D_ {31} & D_ {32} & D_ {33 } \ end {bmatrix} = \ cfrac {2h ^ 3} {3 (1 - \ nu_ {12} \ {21} nu_)} \ begin {bmatrix} E_1 & \ nu_ {12} E_2 & 0 \ \ \ nu_ {21} E_1 & E_2 & 0 \ \ 0 & 0 & 2G_ {12} (1 - \ nu_ {12} \ {21} nu_) \ end {bmatrix} \,.

    Pembebanan transversal

    Persamaan yang mengatur piring Kirchhoff orthotropic dimuat melintang oleh beban didistribusikan q per satuan luas adalah
    D_x w ^ 0_ {, 1111} + 2 D_ {xy} w ^ 0_ {, 1122} + D_y w ^ 0_ {, 2222} =-q
    dimana
    \ Begin {} menyelaraskan D_x & = D_ {11} = \ frac {2h ^ 3 E_1} {3 (1 - \ nu_ {12} \ {21} nu_)} \ \ D_y & = D_ {22} = \ frac {2h ^ 3 E_2} {3 (1 - \ nu_ {12} \ {21} nu_)} \ \ D_ {xy} & = D_ {33} + \ tfrac {1} {2} (\ nu_ {21} D_ {11} + \ nu_ {12} {22} D_) = D_ {33} + \ nu_ {21} {11} D_ = \ frac {4h ^ 3 G_ {12}} {3} + \ frac {2h ^ 3 \ nu_ {21}} {E_1 3 (1 - \ nu_ {12} \ {21} nu_)} \,. \ End {} menyelaraskan

    Dinamika tipis pelat Kirchhoff

    Artikel utama: Kirchhoff-Love teori pelat
    Teori dinamis pelat menentukan propagasi gelombang di piring, dan studi gelombang berdiri dan mode getaran.

    Persamaan Pemerintahan

    Persamaan yang mengatur untuk dinamika piring Kirchhoff-Love adalah
    \ Begin {} menyelaraskan n_ {\ alpha \ beta, \ beta} & = J_1 ~ \ ddot {u} ^ 0_ \ alpha \ \ M_ {\ alpha \ beta, \ alpha \ beta} - q (x, t) & = J_1 ~ \ ddot {w} ^ 0 - J_3 ~ \ ddot {w} ^ {0_, \ alpha \ alpha} \ end {} menyelaraskan
    di mana, untuk piring dengan kepadatan \ Rho = \ rho (x) ,
    J_1: = \ int_ {-h} ^ h \ rho ~ dx_3 = 2 ~ \ rho ~ h ~; ~ ~ J_3: = \ int_ {-h} ^ h x_3 ^ 2 ~ \ rho ~ dx_3 = \ frac {2} {3} ~ \ rho ~ h ^ 3
    dan
    \ Dot {u} _i = \ frac {\ u_i parsial} {\ partial t} ~; ~ ~ \ Ddot {u} _i = \ frac {\ partial ^ 2 u_i} {\ partial t ^ 2} ~; ~ ~ U_ {i, \ alpha} = \ frac {\ u_i parsial} {\ partial x_ \ alpha} ~; ~ ~ U_ {i, \ alpha \ beta} = \ frac {\ partial ^ 2 u_i} {\ x_ parsial \ alpha \ parsial x_ \ beta}
    Angka-angka di bawah ini menunjukkan beberapa mode getaran dari piring melingkar.
  • Modus k = 0, p = 1
  • Modus k = 1, p = 2

Pelat isotropik

Persamaan yang mengatur menyederhanakan cukup untuk isotropik dan homogen piring yang di-pesawat deformasi dapat diabaikan dan memiliki bentuk
D \, \ left (\ frac {\ partial ^ 4 w ^ 0} {\ x_1 parsial ^ 4} + 2 \ frac {\ partial ^ 4 w ^ 0} {\ x_1 parsial ^ 2 \ x_2 parsial ^ 2} + \ frac {\ partial ^ 4 w ^ 0} {\ x_2 parsial ^ 4} \ right) =-q (x_1, x_2, t) - 2 \ rho h \, \ frac {\ partial ^ 2 w ^ 0} { \ parsial t ^ 2} \,.
dimana D adalah kekakuan lentur dari piring. Untuk piring seragam ketebalan 2h ,
D: = \ cfrac {2h ^ 3E} {3 (1 - \ nu ^ 2)} \,.
Dalam notasi langsung
D \, \ nabla ^ 2 \ nabla ^ 2 w ^ 0 =-q (x, y, t) - 2 \ rho h \, \ ddot {w} ^ 0 \,.

Teori Mindlin-Reissner untuk pelat tebal

Artikel utama: Mindlin-Reissner teori pelat
Catatan: Einstein penjumlahan konvensi penjumlahan pada indeks berulang digunakan di bawah ini.
Dalam teori pelat tebal, atau teori Raymond Mindlin [4] dan Eric Reissner , normal sampai pertengahan-permukaan tetap lurus tetapi tidak harus tegak lurus terhadap pertengahan permukaan. Jika \ Varphi_1 dan \ Varphi_2 menunjuk sudut yang pertengahan permukaan membuat dengan x_3 axis kemudian
\ Varphi_1 \ ne W_ {, 1} ~; ~ ~ \ Varphi_2 \ ne W_ {, 2}
Maka hipotesis Mindlin-Reissner menyiratkan bahwa
\ Begin {} menyelaraskan u_ \ alpha (\ mathbf {x}) & = u ^ 0_ \ alpha (x_1, x_2) - x_3 ~ \ varphi_ \ alpha ~; ~ ~ \ Alpha = 1,2 \ \ u_3 (\ mathbf {x}) & = w ^ 0 (x_1, x_2) \ end {} menyelaraskan

Hubungan regangan-perpindahan

Tergantung pada jumlah rotasi normals pelat dua pendekatan yang berbeda untuk strain dapat diturunkan dari asumsi dasar kinematik.
Untuk strain kecil dan rotasi kecil hubungan regangan-perpindahan untuk pelat Mindlin-Reissner adalah
\ Begin {} menyelaraskan \ varepsilon_ {\ alpha \ beta} & = \ frac {1} {2} (u ^ 0_ {\ alpha, \ beta} + u ^ 0_ {\ beta, \ alpha}) - \ frac { x_3} {2} ~ (\ varphi_ {\ alpha, \ beta} + \ varphi_ {\ beta, \ alpha}) \ \ \ varepsilon_ {\ alpha} 3 & = \ cfrac {1} {2} \ left (w ^ 0_ {, \ alpha} - \ varphi_ \ alpha \ right) \ \ \ varepsilon_ {33} & = 0 \ end {} menyelaraskan
Regangan geser, dan karenanya tegangan geser, seluruh tebal pelat tidak diabaikan dalam teori ini. Namun, regangan geser adalah konstan di seluruh tebal pelat. Hal ini tidak dapat akurat karena tegangan geser diketahui parabola bahkan untuk geometri pelat sederhana. Untuk memperhitungkan ketidaktelitian dalam regangan geser, geser faktor koreksi ( \ Kappa ) Diterapkan sehingga jumlah yang benar energi internal yang diprediksi oleh teori. Kemudian
\ Varepsilon_ {\ alpha 3} = \ cfrac {1} {2} ~ \ kappa ~ \ left (w ^ 0_ {, \ alpha} - \ varphi_ \ alpha \ right)

Persamaan Equilibrium

Persamaan kesetimbangan memiliki bentuk yang sedikit berbeda tergantung pada jumlah lentur diharapkan piring. Untuk situasi di mana strain dan rotasi piring adalah smallthe persamaan kesetimbangan untuk piring Mindlin-Reissner adalah
\ Begin {} menyelaraskan & n_ {\ alpha \ beta, \ alpha} = 0 \ \ & M_ {\ alpha \ beta, \ beta}-Q_ \ alpha = 0 \ \ & Q_ {\ alpha, \ alpha} + q = 0 \,. \ End {} menyelaraskan
Gaya geser yang dihasilkan dalam persamaan di atas didefinisikan sebagai
Q_ \ alpha: = \ kappa ~ \ int_ {-h} ^ h \ sigma_ {\ alpha 3} ~ dx_3 \,.

Kondisi batas

Kondisi batas ditunjukkan oleh ketentuan batas dalam prinsip kerja virtual.
Jika satu-satunya kekuatan eksternal adalah gaya vertikal pada permukaan atas piring, kondisi batas yang
\ Begin {} menyelaraskan n_ \ alpha ~ n_ {\ alpha \ beta} & \ quad \ mathrm {atau} \ quad u ^ 0_ \ beta \ \ n_ \ alpha ~ M_ {\ alpha \ beta} & \ quad \ mathrm { atau} \ quad \ varphi_ \ alpha \ \ n_ \ alpha ~ Q_ \ alpha & \ quad \ mathrm {atau} \ quad w ^ 0 \ end {} menyelaraskan

Hubungan konstitutif

Hubungan tegangan-regangan untuk elastis piring Mindlin-Reissner linear yang diberikan oleh
\ Begin {} menyelaraskan \ sigma_ {\ alpha \ beta} & = C_ {\ alpha \ beta \ gamma \ theta} ~ \ varepsilon_ {\ gamma \ theta} \ \ \ sigma_ {\ alpha} 3 & = C_ {\ alpha 3 \ gamma \ theta} ~ \ varepsilon_ {\ gamma \ theta} \ \ \ sigma_ {33} & = C_ {33 \ gamma \ theta} ~ \ varepsilon_ {\ gamma \ theta} \ end {} menyelaraskan
Karena \ Sigma_ {33} tidak muncul dalam persamaan kesetimbangan secara implisit diasumsikan bahwa itu tidak memiliki efek pada keseimbangan momentum dan diabaikan. Asumsi ini juga disebut asumsi plane stress. Sisanya hubungan tegangan-regangan untuk bahan orthotropic , dalam bentuk matriks, dapat ditulis sebagai
\ Begin {bmatrix} \ {11} sigma_ \ \ \ sigma_ {22} \ \ \ sigma_ {23} \ \ \ sigma_ {31} \ \ \ sigma_ {12} \ end {bmatrix} = \ begin {bmatrix} C_ {11} & C_ {12} & 0 & 0 & 0 \ \ C_ {12} & C_ {22} & 0 & 0 & 0 \ \ 0 & 0 & C_ {44} & 0 & 0 \ \ 0 & 0 & 0 & C_ {55} & 0 \ \ 0 & 0 & 0 & 0 & C_ {66} \ end {bmatrix} \ begin {bmatrix} \ {11} varepsilon_ \ \ \ varepsilon_ {22} \ \ \ varepsilon_ { 23} \ \ \ varepsilon_ {31} \ \ \ varepsilon_ {12} \ end {bmatrix}
Kemudian,
\ Begin {bmatrix} n_ {11} \ \ n_ {22} \ \ n_ {12} \ end {bmatrix} = \ left \ {\ {int_-h} ^ h \ begin {bmatrix} C_ {11} & C_ {12} & 0 \ \ C_ {12} & C_ {22} & 0 \ \ 0 & 0 & C_ {66} \ end {bmatrix} ~ dx_3 \ right \} \ begin {bmatrix} u ^ 0_ {1, 1} \ \ u ^ 0_ {2,2} \ \ \ frac {1} {2} ~ (u ^ 0_ {1,2} + u ^ 0_ {2,1}) \ end {bmatrix}
dan
\ Begin {bmatrix} M_ {11} \ \ M_ {22} \ \ M_ {12} \ end {bmatrix} = - \ left \ {\ {int_-h} ^ h x_3 ^ 2 ~ \ begin {bmatrix} C_ {11} & C_ {12} & 0 \ \ C_ {12} & C_ {22} & 0 \ \ 0 & 0 & C_ {66} \ end {bmatrix} ~ dx_3 \ right \} \ begin {bmatrix} \ varphi_ {1,1} \ \ \ varphi_ {2,2} \ \ \ frac {1} {2} ~ (\ varphi_ {1,2} + \ varphi_ {2,1}) \ end {bmatrix}
Untuk persyaratan geser
\ Begin {bmatrix} Q_1 \ \ Q_2 \ end {bmatrix} = \ cfrac {\ kappa} {2} \ left \ {\ {int_-h} ^ h \ begin {bmatrix} C_ {55} & 0 \ \ 0 & C_ {44} \ end {bmatrix} ~ dx_3 \ right \} \ begin {bmatrix} w ^ 0_ {, 1} - \ varphi_1 \ \ w ^ 0_ {, 2} - \ varphi_2 \ end {bmatrix}
The kekakuan ekstensional adalah jumlah
A_ {\ alpha \ beta}: = \ int_ {-h} ^ h C_ {\ alpha \ beta} ~ dx_3
The kekakuan lentur adalah jumlah
D_ {\ alpha \ beta}: = \ int_ {-h} ^ h x_3 ^ 2 ~ C_ {\ alpha \ beta} ~ dx_3

Isotropik dan homogen piring Mindlin-Reissner

Artikel utama: Mindlin-Reissner teori pelat
Untuk seragam tebal, homogen, isotropik dan pelat, hubungan tegangan-regangan pada bidang piring yang
\ Begin {bmatrix} \ {11} sigma_ \ \ \ sigma_ {22} \ \ \ sigma_ {12} \ end {bmatrix} = \ cfrac {E} {1 - \ nu ^ 2} \ begin {bmatrix} 1 & \ nu & 0 \ \ \ nu & 1 & 0 \ \ 0 & 0 & 1 - \ nu \ end {bmatrix} \ begin {bmatrix} \ {11} varepsilon_ \ \ \ varepsilon_ {22} \ \ \ varepsilon_ {12 } \ end {bmatrix} \,.
dimana E adalah modulus Young, \ Nu adalah rasio Poisson, dan \ Varepsilon_ {\ alpha \ beta} adalah strain dalam pesawat. Melalui-the-ketebalan tegangan geser dan strain terkait dengan
\ Sigma_ {31} = 2G \ varepsilon_ {31} \ quad \ text {Dan} \ quad \ sigma_ {32} = 2G \ varepsilon_ {32}
dimana G = E / (2 (1 + \ nu)) adalah modulus geser .

Hubungan konstitutif

Hubungan antara resultan tegangan dan perpindahan umum untuk pelat Mindlin-Reissner isotropik adalah:
\ Begin {bmatrix} n_ {11} \ \ n_ {22} \ \ n_ {12} \ end {bmatrix} = \ cfrac {2EH} {1 - \ nu ^ 2} \ begin {bmatrix} 1 & \ nu & 0 \ \ \ nu & 1 & 0 \ \ 0 & 0 & 1 - \ nu \ end {bmatrix} \ begin {bmatrix} u ^ 0_ {1,1} \ \ u ^ 0_ {2,2} \ \ \ frac {1} {2} ~ (u ^ 0_ {1,2} + u ^ 0_ {2,1}) \ end {bmatrix} \,,
\ Begin {bmatrix} M_ {11} \ \ M_ {22} \ \ M_ {12} \ end {bmatrix} = - \ cfrac {2EH ^ 3} {3 (1 - \ nu ^ 2)} \ begin {bmatrix } 1 & \ nu & 0 \ \ \ nu & 1 & 0 \ \ 0 & 0 & 1 - \ nu \ end {bmatrix} \ begin {bmatrix} \ {1,1} varphi_ \ \ \ varphi_ {2,2 } \ \ \ frac {1} {2} (\ varphi_ {1,2} + \ varphi_ {2,1}) \ end {bmatrix} \,,
dan
\ Begin {bmatrix} Q_1 \ \ Q_2 \ end {bmatrix} = \ kappa G h \ begin {bmatrix} w ^ 0_ {, 1} - \ varphi_1 \ \ w ^ 0_ {, 2} - \ varphi_2 \ end {bmatrix } \,.
The kekakuan lentur didefinisikan sebagai kuantitas
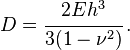
D = \ cfrac {2EH ^ 3} {3 (1 - \ nu ^ 2)} \,.
Untuk sepiring ketebalan h , Kekakuan lentur memiliki bentuk
D = \ cfrac {Eh ^ 3} {12 (1 - \ nu ^ 2)} \,.

Persamaan Pemerintahan

Jika kita mengabaikan ekstensi di-pesawat piring, persamaan yang mengatur adalah
\ Begin {} menyelaraskan M_ {\ alpha \ beta, \ beta}-Q_ \ alpha & = 0 \ \ Q_ {\ alpha, \ alpha} + q = 0 & \,. \ End {} menyelaraskan
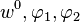
Dalam hal deformasi umum w ^ 0, \ varphi_1, \ varphi_2 , Tiga persamaan yang mengatur adalah
\ {MULAI menyelaraskan} & \ nabla ^ 2 \ left (\ frac {\ partial \ varphi_1} {\ x_1 parsial} + \ frac {\ partial \ varphi_2} {\ x_2 parsial} \ right) = - \ frac {q} {D} \ \ & \ nabla ^ 2 w ^ 0 - \ frac {\ partial \ varphi_1} {\ partial} x_1 - \ frac {\ partial \ varphi_2} {\ x_2 parsial} = - \ frac {q} {\ kappa G h} \ \ & \ nabla ^ 2 \ left (\ frac {\ partial \ varphi_1} {\ x_2 parsial} - \ frac {\ partial \ varphi_2} {\ x_1 parsial} \ right) = - \ frac {2 \ kappa G h} {D (1 - \ nu)} \ left (\ frac {\ partial \ varphi_1} {\ x_2 parsial} - \ frac {\ partial \ varphi_2} {\ x_1 parsial} \ right) \,. \ End {} menyelaraskan
Kondisi batas sepanjang tepi piring persegi panjang adalah
\ Begin {menyelaraskan} \ text {HANYA didukung} \ quad & \ quad w ^ 0 = 0, M_ {11} = 0 ~ (\ text {} atau ~ M_ {22} = 0), \ varphi_1 = 0 ~ ( \ text {} atau ~ \ varphi_2 = 0) \ \ \ text {dijepit} \ quad & \ quad w ^ 0 = 0, \ varphi_1 = 0, \ varphi_ {2} = 0 \,. \ End {} menyelaraskan

Teori Reissner-Stein untuk isotropik pelat kantilever

Secara umum, solusi yang tepat untuk plat kantilever menggunakan teori plat cukup terlibat dan solusi yang tepat beberapa dapat ditemukan dalam literatur. Reissner dan Stein [5] memberikan teori disederhanakan untuk pelat kantilever yang merupakan perbaikan atas teori-teori yang lebih tua seperti Saint-Venant teori lempeng.
The Reissner-Stein teori mengasumsikan bidang perpindahan melintang dalam bentuk
w (x, y) = w_x (x) + y \, \ theta_x (x) \,.
Persamaan yang mengatur untuk piring kemudian mengurangi dua ditambah persamaan diferensial biasa:
\ Begin {} menyelaraskan & bD \ frac {\ mathrm {d} ^ 4w_x} {\ mathrm {d} x ^ 4} = Q_1 (x) - n_1 (x) \ cfrac {d ^ 2} {dx w_x ^ 2 } - \ cfrac {d} {dx n_1} \, \ cfrac {d} {dx} w_x - \ frac {1} {2} \ cfrac {d} {dx n_2} \, \ cfrac {d \ theta_x} { dx} - \ frac {n_2 (x)} {2} \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} \ \ & \ frac {b ^ 3D} {12} \, \ frac {\ mathrm {d } ^ 4 \ theta_x} {\ mathrm {d} x ^ 4} - 2BD (1 - \ nu) \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} = q_2 (x) - n_3 (x) \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} - \ cfrac {d} {dx n_3} \, \ cfrac {d \ theta_x} {dx} - \ frac {n_2 (x)} {2} \, \ cfrac {d ^ 2} {dx w_x ^ 2} - \ frac {1} {2} \ cfrac {d} {dx n_2} \, \ cfrac {d} {dx} w_x \ end {} menyelaraskan
dimana
\ Begin {} menyelaraskan Q_1 (x) & = \ int_ {-b / 2} ^ {b / 2} q (x, y) \, \ text {d} y ~, ~ ~ q_2 (x) = \ int_ {-b / 2} ^ {b / 2} y \, q (x, y) \, \ text {d} y ~, ~ ~ n_1 (x) = \ int_ {-b / 2} ^ {b / 2} n_x (x, y) \, \ text {d} y \ \ n_2 (x) & = \ int_ {-b / 2} ^ {b / 2} y \, n_x (x, y) \, \ text {d} y ~, ~ ~ n_3 (x) = \ int_ {-b / 2} ^ {b / 2} y ^ 2 \, n_x (x, y) \, \ text {d} y \,. \ End {} menyelaraskan
Di x = 0 , Karena balok dijepit, kondisi batas yang
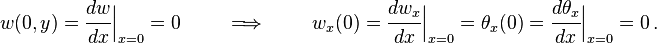
w (0, y) = \ cfrac {} {dx dw} \ Bigr | _ {x = 0} = 0 \ qquad \ menyiratkan \ qquad w_x (0) = \ cfrac {d} {dx} w_x \ Bigr | _ {x = 0} = \ theta_x (0) = \ cfrac {d \ theta_x} {dx} \ Bigr | _ {x = 0} = 0 \,.
Kondisi batas pada x = a adalah
\ Begin {} menyelaraskan & bD \ cfrac {d ^ 3 w_x} {dx ^ 3} + n_1 (x) \ cfrac {d} {dx} + w_x n_2 (x) \ cfrac {d \ theta_x} {dx} + Q_ {x1} = 0 \ \ & \ frac {b ^ 3D} {12} \ cfrac {d ^ 3 \ theta_x} {dx ^ 3} + \ left [n_3 (x)-2BD (1 - \ nu) \ kanari] \ cfrac {d \ theta_x} {dx} + n_2 (x) \ cfrac {d} {dx} + w_x t = 0 \ \ & bD \ cfrac {d ^ 2} {dx w_x ^ 2} + m_1 = 0 \ quad, \ quad \ frac {b ^ 3D} {12} \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} + m_2 = 0 \ end {} menyelaraskan
dimana
\ Begin {} menyelaraskan m_1 & = \ int_ {-b / 2} ^ {b / 2} m_x (y) \, \ text {d} y ~, ~ ~ m_2 = \ int_ {-b / 2} ^ { b / 2} y \, m_x (y) \, \ text {d} y ~, ~ ~ Q_ {x1} = \ int_ {-b / 2} ^ {b / 2} q_x (y) \, \ text {d} y \ \ t & = Q_ {x2} + m_3 = \ int_ {-b / 2} ^ {b / 2} y \, q_x (y) \, \ text {d} y + \ int_ {- b / 2} ^ {b / 2} m_ {xy} (y) \, \ text {d} y \,. \ End {} menyelaraskan

Referensi

  1. Timoshenko, S. dan Woinowsky-Krieger, S. "Teori piring dan kerang". McGraw-Hill New York, 1959.
  2. AEH Love, On getaran bebas kecil dan deformasi kerang elastis, Philosophical trans. dari Royal Society (London), 1888, Vol. série A, N ° 17 p. 491-549.
  3. Reddy, JN, 2007, Teori dan analisis pelat elastis dan kerang, CRC Press, Taylor dan Francis.
  4. RD Mindlin, Pengaruh inersia berputar dan geser pada gerakan lentur isotropik, pelat elastis, Journal of Applied Mechanics, 1951, Vol. 18 p. 31-38.
  5. E. Reissner dan M. Stein. Torsi dan lentur melintang dari pelat kantilever. Catatan Teknis 2369, Komite Penasihat Nasional untuk Aeronautics, Washington, 1951.

  •  


     

 

Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)